Compact objects in D(R)

28 Jul

Compact objects in D(R)

Posted July 28, 2011 by wrathofrog in Homological algebra. 1 Comment

Section 1. Perfect complexes in 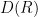$D(R)$

Let $R$ be a commutative Noetherian ring with identity. A chain complex $P\in D(R)$ is called perfect if it is bounded and finitely generated projective in each dimension, i.e. $P\in D_{\mathrm{perf}}(R)$ . Recall that an object $c$ in a triangulated category is compact if the functor $\mathrm{Hom}(c,-)$ preserves all coproducts. Observe that this property is equivalent to the statement:

Every map has its image in finitely many factors of the coproducts. ( $\ast$ )

The following gives us an example non-compact object in $D(k)$ .

Example. An infinite dimensional $k$ -vector space $V$ with a countable basis $\{e_1,e_2,e_3,...\}$ can be treated as an unbounded chain complex of finitely generated free modules over $k$ . Consider the identity map $id_V:V\rightarrow V$ which is an element in $\mathrm{Hom}_k(V,V)$ . Let $V_i=\langle e_i\rangle$ for each $i=1,2,3,...$ . Suppose $id_V\in\bigoplus \mathrm{Hom}_k(V,V_i)$ , then there is a finite subset $\{i_1,i_2,...,i_n\}\subseteq\{1,2,3,...\}$ and finitely many maps $f_{i_j}:V\rightarrow V_{i_j}$ such that $id_V=\bigoplus_{j=1}^n f_{i_j}$ . This is absurd since they have images as

$\mathrm{Im}(\bigoplus_{j=1}^n f_{i_j})\subseteq \bigoplus_{j=1}^nV_{i_j}\neq V$

while $\mathrm{Im}~id_V=V$ . In particular, the functor $\mathrm{Hom}_k(V,-)$ does not preserve direct sums.

Lemma 1. Let $P$ be a projective $R$ -module. Then $P$ is finitely generated if and only if the functor $\mathrm{Hom}_R(P,-)$ preserves all direct sums.

Proof. This is in the proof of Proposition 1.2. (c) in [3]. Let $Y=\bigoplus_{i\in I} Y_i$ be a direct sum of $R$ -modules and $f:P\rightarrow Y$ be an $R$ -module map. Since $P$ is finitely generated, $f$ is determined by the images of its finitely many generators hence $\mathrm{Im}f$ lies in finitely many summands in $Y$ . Hence the observation ( $\ast$ ) imply the sufficiency (Notice that we do not use the assumption that $P$ is projective). Conversely, suppose $P$ is a direct summand of a free module $\bigoplus_{j\in J}R_j$ where each $R_j=R$ , i.e. there is an injection $f:P\rightarrow \bigoplus_{j\in J}R_j$ . Hence the image $\mathrm{Im}f$ lies in $\bigoplus_{i\in I}R_i$ for some finite subset $I\subseteq J$ . Therefore, $P\cong \mathrm{Im}f$ is finitely generated. $\square$

Recall that direct sum (resp. direct product) of chain complexes of $R$ -modules is defined degreewisely, thus the homology functor commutes with direct sums (resp. direct product). Also, for every bounded below chain complex of $R$ -modules $P$ we have

$\mathrm{Hom}_{D(R)}(P,\Sigma^nN)\cong H_n(\mathbf{Hom}_R(P,N))$ ( $\ast\ast$ )

for every $N\in D(R)$ and every $n\in\mathbb{Z}$ .

Lemma 2. Every finitely generated projective $R$ -module is compact in $D(R)$ .

Proof. Suppose $P$ is a finitely generated projective $R$ -module and $Y=\bigoplus Y_i$ is a direct sum in $D(R)$ . Since $P$ is projective we deduce that $\mathrm{Hom}_{D(R)}(P,Y)\cong H_0(\mathbf{Hom}_R(P,Y))$ and $\bigoplus\mathrm{Hom}_{D(R)}(P,Y_i)\cong\bigoplus H_0(\mathbf{Hom}_R(P,Y_i))\cong H_0(\bigoplus\mathbf{Hom}_R(P,Y_i))$ . Thus it suffices to show that the two total Hom chain complexes are isomorphic by comparing each degree, i.e.

$\mathbf{Hom}_R(P,Y)\cong\bigoplus_i\mathbf{Hom}_R(P,Y_i)$ .

In fact, on degree $q$ we have by Lemma 1

$\mathrm{Hom}_R(P,Y_q)=\mathrm{Hom}_R(P,\bigoplus_i(Y_i)_q)\cong\bigoplus_i\mathrm{Hom}_R(P,(Y_i)_q)$

as required. $\square$

Proposition 3. The perfect complexes in $D(R)$ are compact.

Proof. Let $P$ be a bounded chain complex of finitely generated projective $R$ -modules and $Y=\bigoplus_iY_i$ be an arbitrary direct sum in $D(R)$ . We claim that

$\mathbf{Hom}_R(P,Y)\cong\bigoplus_i\mathbf{Hom}_R(P,Y_i)$ ,

thus particularly $\mathrm{Hom}_{D(R)}(P,Y)\cong\bigoplus_i\mathrm{Hom}_{D(R)}(P,Y_i)$ by using the property ( $\ast\ast$ ) and the fact that homology functors commute with direct sums. We still compare the two total Hom chain complexes degreewisely. In fact, consider the $n$ -th degree and bear in mind that $P$ is bounded, we deduce that

$\displaystyle \prod_{p+q=n}\mathrm{Hom}_R(P_{-p},Y_q)\cong\bigoplus_{p+q=n}\mathrm{Hom}_R(P_{-p},\bigoplus_i(Y_i)_q)\cong \bigoplus_{p+q=n,i}\mathrm{Hom}_R(P_{-p},(Y_i)_q)$

and $\displaystyle \bigoplus_i\prod_{p+q=n}\mathrm{Hom}_R(P_{-p},(Y_i)_q)\cong\bigoplus_{p+q=n,i}\mathrm{Hom}_R(P_{-p},(Y_i)_q)$ , as required. $\square$

Remark A. There is another approach of proving Proposition 3 by using Lemma 2 and distinguished triangles. Indeed, by using the standard homology truncation of the bounded complex $P$ , we have a finite collection of distinguished triangles

$0=P_{-1}\rightarrow P_0\rightarrow P_1\rightarrow\cdots\rightarrow P_{n-1}\rightarrow P_n=P$

such that each of their third edges say, is $\Sigma^iH_i(P)$ . Clearly, $\mathrm{Hom}_{D(R)}(P_{-1},-)$ preserves direct sums. Hence inductively we have for each $i\geqslant 0$ and each direct sum $Y=\bigoplus Y_j$ in $D(R)$ a long exact sequence by applying $\mathrm{Hom}_{D(R)}(-,Y)$ to the distinguished triangles,

$\displaystyle\begin{matrix}[\Sigma^iH_{i+1},Y]&\rightarrow &[P_i,Y]&\rightarrow &[P_{i+1},Y]&\rightarrow&[\Sigma^{i+1}H_{i+1},Y]&\rightarrow&[\Sigma P_i,Y]\\\|&&\|&&\downarrow&&\|&&\|\\ [\Sigma^iH_{i+1},Y_j]^j&\rightarrow &[P_i,Y_j]^j&\rightarrow &[P_{i+1},Y_j]^j&\rightarrow&[\Sigma^{i+1}H_{i+1},Y_j]^j&\rightarrow&[P_i,Y_j]^j\end{matrix}$

such that all the vertical maps but the middle one are isomorphisms, where $[P_i,Y_j]^j=\bigoplus_j\mathrm{Hom}_{D(R)}(P_i,Y_j)$ and $H_i=H_i(P)$ . Then Five-Lemma implies that the middle one is also an isomorphism, i.e. $\mathrm{Hom}_{D(R)}(P_{i+1},Y)\cong\bigoplus_j\mathrm{Hom}_{D(R)}(P_{i+1},Y_j)$ . In particular, $\mathrm{Hom}_{D(R)}(P,-)$ commutes with direct sums.

Section 2. Localizing subcategories and local objects

For the remaining of this post, I would like to present the proof of the converse of Proposition 3, following the outline of Lemma 2.2 in [1]. As a preliminary, we recall some related but useful concepts.

Let $\mathcal{T}$ be a triangulated category closed under all small coproducts and $\mathcal{L}$ be a full triangulated subcategory of $\mathcal{T}$ . We say that $\mathcal{L}$ is a thick subcategory if it is closed under retracts, and $\mathcal{L}$ is a localizing subcategory if it is closed under coproducts. The following proposition implies that every localizing subcategory is thick.

Proposition 4. Every idempotent in a triangulated category $\mathcal{T}$ which is closed under coproducts splits in $\mathcal{T}$ .

Proof. This is Proposition 3.2 in [5]. Suppose $e:X\rightarrow X$ is an idempotent in $\mathcal{T}$ . Then consider $Y=\underrightarrow{\mathrm{hocolim}}\{X\stackrel{e}{\rightarrow}X\stackrel{e}{\rightarrow}\cdots\}$ and $Z=\underrightarrow{\mathrm{hocolim}}\{X\stackrel{1-e}{\rightarrow}X\stackrel{1-e}{\rightarrow}\cdots\}$ . Clearly, both of $Y$ and $Z$ lie in $\mathcal{T}$ . Observe that $\varphi=\displaystyle\begin{pmatrix}e&1-e\\1-e&e\end{pmatrix}$ plays a role of chain map in the following commutative diagram, and the homotopy colimit of the bottom row is precisely $X$ .

$\displaystyle\begin{matrix}X\bigoplus X&\stackrel{\mathrm{diag}(e,1-e)}{\longrightarrow}&X\bigoplus X&\stackrel{\mathrm{diag}(e,1-e)}{\longrightarrow} &\cdots\\ \downarrow^{\varphi}&&\downarrow^{\varphi}&&\\ X\bigoplus X&\stackrel{\mathrm{diag}(1,0)}{\longrightarrow}&X\bigoplus X&\stackrel{\mathrm{diag}(1,0)}{\longrightarrow}&\cdots \end{matrix}$

Furthermore, one can check that $\varphi^2=1$ . Hence $X\cong Y\bigoplus Z$ as required. $\square$

Construction of quotient categories. Let $\mathcal{T}$ be a triangulated category closed under coproducts and $T$ be a set of compact objects in $\mathcal{T}$ such that $T$ is closed under suspension. Then let $\mathcal{L}$ be the smallest localizing subcategory of $\mathcal{T}$ containing $T$ . Then we can form the quotient category $\mathcal{T/L}$ together with a natural functor $j^\ast:\mathcal{T}\rightarrow\mathcal{T/L}$ . We define an object $Y\in\mathcal{T}$ to be $T$ –local if $\mathrm{Hom}_\mathcal{T}(T,Y)=0$ .

Lemma 5. For each $T$ -local object $Y\in \mathcal{T}$ , we have $\mathrm{Hom}_\mathcal{T}(X,Y)\cong\mathrm{Hom}_\mathcal{T/L}(X,Y)$ .

Proof. Consider morphisms in the category $T$ . Suppose $X'\stackrel{\alpha}{\rightarrow} X\rightarrow Z$ is a distinguished triangle with $Z\in \mathcal{L}$ . Then applying the functor $\mathrm{Hom}_\mathcal{T}(-,Y)$ , we obtain an exact sequence

$0=\mathrm{Hom}_\mathcal{T}(Z,Y)\rightarrow \mathrm{Hom}_\mathcal{T}(X,Y)\stackrel{\alpha^\ast}{\rightarrow}\mathrm{Hom}_\mathcal{T}(X',Y)\rightarrow \mathrm{Hom}_\mathcal{T}(\Sigma^{-1}Z,Y)=0$

which says that $\alpha^\ast$ is an isomorphism. Since every morphism in $\mathcal{T/L}$ is of the form $X\stackrel{\alpha}{\leftarrow} X'\rightarrow Y$ with $\alpha$ a quasi-isomorphism, i.e. its mapping cone is an object in $\mathcal{L}$ , the previous argument implies that $\mathrm{Hom}_\mathcal{T}(X,Y)\rightarrow\mathrm{Hom}_\mathcal{T/L}(X,Y)$ is surjective. For the injectivity, suppose $f:X\rightarrow Y$ in $\mathcal{T}$ is mapped to zero in $\mathcal{T/L}$ . Then $f$ factors as $f:X\rightarrow Z\rightarrow Y$ with $Z\in\mathcal{L}$ , hence $f=0$ since $Y$ is $T$ -local. $\square$

The next lemma says that every object in $\mathcal{T}$ is quasi-isomorphic to a $T$ -local objects.

Proposition 6. Let $\mathcal{T}$ be a triangulated category closed under coproducts and $T$ be a set of compact objects in $\mathcal{T}$ . Then for every object $X\in \mathcal{T}$ , there is a $T$ -local object $Y\in\mathcal{T}$ and a morphism $f:X\rightarrow Y$ such that its mapping cone lies in the smallest localizing subcategory $\mathcal{L}\subseteq\mathcal{T}$ containing $T$ .

Proof. Let $X_0=X$ and $U_i=\{f:t\rightarrow X_i~|~t\in T\}=\{(f,t)~|~t\in T,~f:t\rightarrow X_i\}$ . Define inductively $X_{i+1}$ as the third edge of the distinguished triangle

$\displaystyle\bigoplus_{(f,t)\in U_i}t\rightarrow X_i\stackrel{\mu_i}{\rightarrow} X_{i+1}$ .

Clearly, the mapping cone of $\mu_i$ lies in $\mathcal{L}$ hence it is an isomorphism in $\mathcal{T/L}$ . Then we define $Y=\underrightarrow{\mathrm{hocolim}}X_i$ . In particular, the structure map $X=X_0\rightarrow Y$ is an isomorphism in $\mathcal{T/L}$ since each $\mu_i$ is.

Now let $t\in T$ be a compact object. Since $\mathrm{Hom}(t,Y)\cong\underrightarrow{\lim}~\mathrm{Hom}(t,X_i)$ (see Lemma 1 in Grothendieck duality) and the fact that every morphism $t\rightarrow X_i$ factors through $\bigoplus\limits_{(f,t)\in U_i}t$ , we deduce that each induced map $(\mu_i)_\ast:\mathrm{Hom}(t,X_i)\rightarrow \mathrm{Hom}(t,X_{i+1})$ is zero so that $\underrightarrow{\lim}~\mathrm{Hom}(t,X_i)=0$ . Therefore, $\mathrm{Hom}(t,Y)=0$ and $Y$ is $T$ -local. $\square$

Remark B. Combing Lemma 5 and 6, we deduce that the functor $j^\ast$ restricted onto the full subcategory $\mathcal{S}$ of all $T$ -local objects in $\mathcal{T}$ is an equivalence of categories from $\mathcal{S}\rightarrow \mathcal{T/L}$ so that it has the inclusion functor $j_\ast:\mathcal{S}\rightarrow \mathcal{T}$ as its right adjoint, which is called Bousfield localization functor. In particular, the counit of adjunction $X\rightarrow j_\ast j^\ast X$ coincides with the map $f:X\rightarrow Y$ in Proposition 6. Explicitly, from its proof we derive that

$j_\ast j^\ast X=\underrightarrow{\mathrm{hocolim}}X_i$ .

Proposition 7. The functor $j_\ast:\mathcal{T/L}\rightarrow\mathcal{T}$ preserves coproducts.

Proof. By virtue of Remark B, it suffices to show that coproduct of $T$ -local objects remains $T$ -local. Indeed, suppose $Y=\bigoplus_i Y_i$ with each $Y_i$ a $T$ -local object. Then $\mathrm{Hom}(t,Y)\cong\bigoplus_i\mathrm{Hom}(t,Y_i)=0$ since $t$ is compact. $\square$

As an application we have the following property of the natural functor $j^\ast$ .

Lemma 8. The restriction of the natural functor $j^\ast: \mathcal{T}^c\rightarrow (\mathcal{T/L})^c$ is well-defined.

Proof. Suppose $Y=\bigoplus_iY_i$ is a coproduct in $\mathcal{T/L}$ and $t\in\mathcal{T}^c$ . Then

$\mathrm{Hom}(j^\ast(t),Y)\cong \mathrm{Hom}(t,j_\ast(Y))\cong \mathrm{Hom}(t,\bigoplus_i j_\ast (Y_i))$

$\cong\bigoplus_i\mathrm{Hom}(t,j_\ast(Y_i))\cong\bigoplus_i\mathrm{Hom}(j^\ast(t),Y_i)$ .

The first and last isomorphism are the adjunctions while the second one is Proposition 7 and the third one is our assumption on $t$ . $\square$

Section 3. Compact objects in 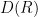$D(R)$

In order to prove Proposition 10, which is the key ingredient of proving Proposition 11, we need the following technical lemma. Before starting, we introduce some notations and assumptions.

Suppose $\mathcal{T}$ is a compactly generated triangulated category which is closed under small coproducts. In other words, the smallest localizing subcategory containing the full subcategory $\mathcal{T}^c$ of compact objects is $\mathcal{T}$ itself. Let $T$ be a subset of $\mathcal{T}^c$ which is closed under suspensions and $\mathcal{L}$ be the smallest localizing subcategory of $\mathcal{T}$ containing $T$ . Denote by $\mathcal{C}_T$ the smallest thick subcategory containing $T$ .

Lemma 9. Let $X\rightarrow Y$ be a morphism in $\mathcal{T}$ with $X\in\mathcal{L}^c$ . Suppose $Y'\rightarrow Y$ is a morphism in $\mathcal{T}$ such that its mapping cone is a finite extension of coproducts in $T$ . Then there is morphism $X'\rightarrow X$ with its mapping cone in $\mathcal{C}_T$ and a morphism $X'\rightarrow Y'$ such that the following diagram

$\displaystyle \begin{matrix}X' &\rightarrow&X\\\downarrow&&\downarrow\\ Y'&\rightarrow&Y\end{matrix}$

is commutative.

Proof. This is Lemma 2.3 in [1]. Suppose $E$ is the mapping cone of $Y'\rightarrow Y$ . Since each object in $\mathcal{C}_T$ is a finite extension of coproducts of objects in $T$ , we prove it by induction on the length of extension of $E$ . Now suppose $E$ is a coproduct of objects in $T$ .

$\displaystyle\begin{matrix}X'&\rightarrow &X&\rightarrow &F\\ \downarrow&&\downarrow&&\downarrow\\ Y'&\rightarrow&Y&\rightarrow &E\end{matrix}$

Since $X$ is compact in $\mathcal{L}$ , the composition $X\rightarrow Y\rightarrow E$ factors through a finite coproduct $F$ which is a direct summand of $E$ . In particular, $F\in\mathcal{C}_T$ . Then by completing the right square into a morphism between two distinguished triangles, we obtain the commutativity of the left square.

Now suppose $E$ has length of extension $n\geqslant 1$ . By the Octahedral Axiom of triangulated category, the morphism $Y'\rightarrow Y$ can be factored into two morphism $Y'\rightarrow Y''\rightarrow Y$ such that each one has its mapping cone of extension length strictly less than $n$ . Hence by induction,

$\displaystyle\begin{matrix}X'&\rightarrow &X''&\rightarrow &X\\ \downarrow&&\downarrow&&\downarrow\\ Y'&\rightarrow&Y''&\rightarrow &Y\end{matrix}$

we derive two morphisms $X'\rightarrow X''$ and $X''\rightarrow X$ as the above diagram shows such that each of their mapping cones lies in $\mathcal{C}_T$ and the diagram commutes. By the Octahedral Axiom again, we deduce that the mapping cone of the composition $X'\rightarrow X''\rightarrow X$ also lies in $\mathcal{C}_T$ . $\square$

Proposition 10. The category $\mathcal{L}^c$ is the smallest thick subcategory containing $T$ . In particular, every compact object in $\mathcal{L}$ is compact in $\mathcal{T}$ , i.e. $\mathcal{L}^c\subseteq \mathcal{T}^c$ .

Proof. This is Lemma 2.2 in [1]. It suffices to show that every $X\in\mathcal{L}^c$ is contained in the smallest thick subcategory $\mathcal{C}_T\subseteq\mathcal{T}$ containing $T$ since every object in $\mathcal{C}_T$ is already compact in $\mathcal{L}$ by definition.

By the construction in the proof of Proposition 6, we have $X_0=X\in\mathcal{L}$ and also $X_i\in\mathcal{L}$ for each $i\geqslant 1$ . Denote by $Z=\underrightarrow{\mathrm{hocolim}}X_i$ . Notice that $Z$ is $T$ -local. Thus Lemma 5 implies that

$0=\mathrm{Hom}_\mathcal{T/L}(X,Z)\cong\mathrm{Hom}_\mathcal{T}(X,Z)\cong\mathrm{Hom}_\mathcal{L}(X,Z)\cong\underrightarrow{\lim}~\mathrm{Hom}_\mathcal{L}(X,X_i)$ ,

since $\mathcal{L}\subseteq \mathcal{T}$ is a full subcategory and $X$ is compact in $\mathcal{L}$ . Hence there is some $X_n$ such that $\eta_n:X_0=X\rightarrow X_n$ is the zero map. In particular, the mapping cone of $\eta_n$ is a finite extension of coproducts in $T$ by the construction of $X_n$ . Also notice that the mapping cone of $\eta_n=0$ is a direct sum $\Sigma X\bigoplus X_n$ . Therefore, $X$ is a direct summand of $Y$ , a finite extension of coproducts in $T$ .

Now suppose $f:X\rightarrow Y$ is our monomorphism with splitting map $g:Y\rightarrow X$ . Thanks to Lemma 9, by assuming $Y'=0$ there is a map $h:X'\rightarrow X$ such that its mapping cone $F\in\mathcal{C}_T$ and $fh=0$ . Thus $h=(gf)h=0$ , hence $X$ is a direct summand of $F$ thus $X\in\mathcal{C}_T$ . $\square$

Proposition 11. Every compact object in $D(R)$ is a perfect complex.

Proof. This is Lemma 4.3 in [4]. Let $T=\{\Sigma^iR~|~i\in\mathbb{Z}\}$ and $\mathcal{L}$ be the smallest localizing subcategory of $D(R)$ containing $T$ . It is clear that $D(R)$ is compactly generated by $T$ . Then Proposition 10 says that $\mathcal{L}^c$ is the smallest thick subcategory containing $T$ hence $\mathcal{L}^c\subseteq D_{\mathrm{perf}}(R)$ since $D_{\mathrm{perf}}(R)$ is clearly a thick subcategory containing $T$ , while Proposition 3 implies that $D_{\mathrm{perf}}(R)\subseteq\mathcal{L}^c$ . Hence they are equal. $\square$

References

[1] A. Neeman, The connection between the K-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel.

[2] J. Rickard, Morita theory for derived categories.

[3] H. Bass, Algebraic K-Theory. Mathematics Lecture Notes Series.

[4] Three Spanish guys, Construction of t-structures and equivalences of derived categories.

[5] M. Bokstedt and A. Neeman, Homotopy colimits in triangulated categories.

One response to this post.

Posted by Injective hulls and local objects « Wrathofrog on August 18, 2011 at 9:37 AM

[…] of fact, being closed under direct sums implies being closed under retracts. See Proposition 4 in Compact objects in D(R)) We say is -local if […]

Reply

M	T	W	T	F	S	S
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

Wrathofrog Mathematics and things I like.